Wie kann ich jeden Pfad in einem gerichteten Diagramm auflisten? (C#)

Bitte zeigen Sie mir einfach in die richtige Richtung oder sagen Sie mir, was ich suchen soll:Wie kann ich jeden Pfad in einem gerichteten Diagramm auflisten? (C#)

Ich habe ein "Baum" -Objekt, das "Knoten" -Objekte enthält. (eigentlich heißt es ein gerichteter Graph). Jeder Knoten enthält die Felder string "name" und "list", die die nächsten Knoten enthalten.

Wie kann ich Listen aller möglichen Knotennamen vom Kopfknoten zum Fußknoten erstellen? jede Liste soll einen Weg von Kopf bis Fuß halten. die Anzahl der Knoten von Kopf bis Fuß ist immer die gleiche, dh: 6.

das ist, was der Baum aussieht:

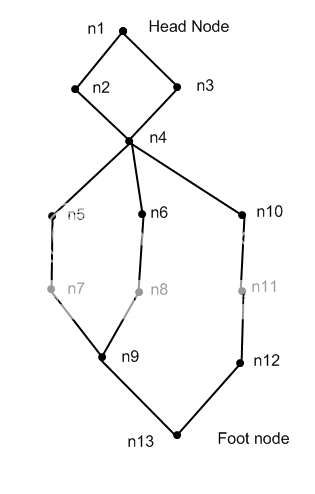
alt text

das Diagramm mir geben soll:

list 1: n1,n2,n4,n5,n7,n9,n13. 
lsit 2: n1,n2,n4,n6,n8,n9,n13. 
list 3: n1,n2,n4,n10,n11,n12,n13

und so weiter.

könnte mir jemand einfach in die richtige richtung zeigen? Welche Art von rekursivem Algorithmus sollte ich verwenden? sollte ich eine rekursive Methode oder nur Schleifen verwenden? (Ich muss dies auf das Ergebnis des Dikstra-Algorithmus verwenden.)

Quelle

2009-06-15 see_sharp_guy

Das ist nicht wirklich ein Baum, oder? –

Angenommen, dies sind Hausaufgaben, bitte nehmen Sie eine Lösung und wir helfen Ihnen weiter. –

Idealerweise würden Sie dafür eine Rekursion verwenden, aber wenn Sie in diesem Diagramm Knoten zu Knoten gehen würden, würden Sie am Ende Pfade wiederholen und in eine Endlosschleife gehen! Sie müssten die Knoten-IDs überprüfen und die Rekursion für diesen Pfad beenden, wenn Sie nur einmal einen Pfad verarbeiten möchten! – OneSHOT

Machen Sie entweder ein BFS oder ein DFS, und verfolgen Sie den Pfad zusammen mit dem Knoten. Wenn der Knoten keine weiteren untergeordneten Elemente aufweist, speichern Sie den Pfad ab. Beachten Sie, dass Sie ein Diagramm/eine Gesamtstruktur anstelle eines Baums haben, aber der Algorithmus, den ich beschrieben habe, funktioniert genauso.

Sie Um zu beginnen ein BFS mit:

Step 1. [n1] 
Step 2. [n2(n1), n3(n1)] 
Step 3. [n3(n1), n4(n1,n2)] 
Step 4. [n4(n1, n2), n4(n1, n3)] 
Step 5. [n4(n1, n3), n5(n1, n2, n4), n6(n1, n2, n4), n10(n1, n2, n4)] 
Step 6. [n5(n1, n2, n4), n6(n1, n2, n4), n10(n1, n2, n4), n5(n1, n3, n4), n6(n1, n3, n4), n10(n1, n3, n4)]

...

und so weiter. Am Ende wirst du deine Wege haben. welches ausgedruckt wird. Sie können diesen Algorithmus implementieren, ohne dass eine Rekursion erforderlich ist. Einfach Schleife, bis das Array leer ist. Macht Sinn?

Quelle

2009-06-15 21:35:21

Danke, das DFS ist genau das, was ich brauchte. Ich implementiere jetzt meine eigene Version davon in C#. wird in wenigen Tagen gepostet, wenn es fertig ist, damit andere es verwenden können. –

Beachten Sie, dass dies nur funktioniert, wenn Ihr Diagramm azyklisch ist und es genau einen "Fuß" -Knoten gibt, der keine Kanten hat. Diese scheinen vernünftige Annahmen zu sein, aber ich würde sie explizit angeben, bevor ich den Auftrag einreiche, wenn ich es wäre. Ohne diese beiden Annahmen sind das Problem und die Lösung komplexer. –

Lösung oben funktioniert für mehrere Fuß Knoten und für verschiedene Tiefen des Baumes, solange er Knoten druckt und entfernt, wenn "Liste" auf den Knoten leer ist. Wird nicht beendet, wenn der Graph einen Zyklus hat. –

Es klingt, als ob Sie nach dem iterator pattern suchen. Dies sollte Sie in die richtige Richtung gehen ...

Quelle

2009-06-15 21:34:37

Das Iteratormuster würde weder in einem Graphen noch in einem gerichteten Graphen funktionieren, außer wenn wir die Bedingung haben, dass jeder Graphknoten nur auf einen anderen zeigen kann. In diesem Fall hätten wir eine einfach verknüpfte Liste. –

Das ist ein Diagramm, kein Baum. http://en.wikipedia.org/wiki/Tree_structure

Also ... mein Zeiger wäre, Sie suchen nach einer Lösung in graph theory. Wenn Sie stecken bleiben, ein bisschen google-fu um diesen Begriff und Ihr Problem sollte Algorithmen zur Umsetzung bringen.

Quelle

2009-06-15 21:36:13 Brabster

In einem gerichteten Diagramm zeigen die Kanten von irgendwo zu irgendwo. In Ihrem Diagramm nicht der Fall. Ihr Graph ist ein ungerichteter Graph. – Brabster

Sie können this wikipedia article hilfreich finden - es beschreibt die verschiedenen Arten von Baum Traversal, die Sie tun können. Am wahrscheinlichsten ist jedoch ein rekursiver Abstieg, Präfix-Traversal. Darüber hinaus ist die Struktur, die Sie beschreiben, kein traditioneller Baum - da er über kreuz-geteilte Knoten verfügt - es ist wahrscheinlich ein Graph. Es gibt auch einige graph traversal Algorithmen. Denken Sie daran, dass, wenn der Graph Zyklen hat, Sie eine Art Zykluserkennung bereitstellen müssen, um die Traversierung zu beenden.

Quelle

2009-06-15 21:38:03 LBushkin

Wie kann ich jeden Pfad in einem gerichteten Diagramm auflisten? (C#)

Antwort

Verwandte Themen